Binary tree data structures consist of nodes who contain some data, point to a parent node and have up to 2 children. Each node is greater than the its child on the left and smaller than its child on the right.
A few reasons why binary trees might be used in place of other data structures including arrays, stacks or queues include:
Below is a complete implementation of a binary tree in JavaScript including functionality for finding nodes, inserting nodes, returning a range of nodes, deleting nodes, keeping track of the size, height and depth of nodes, and keeping the trees balanced and AVL compliant for efficiency purposes.
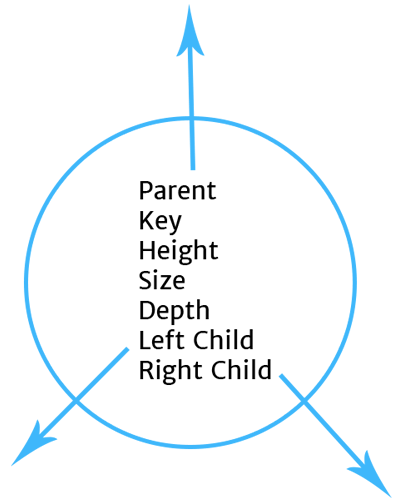
Here is what each node will look like:
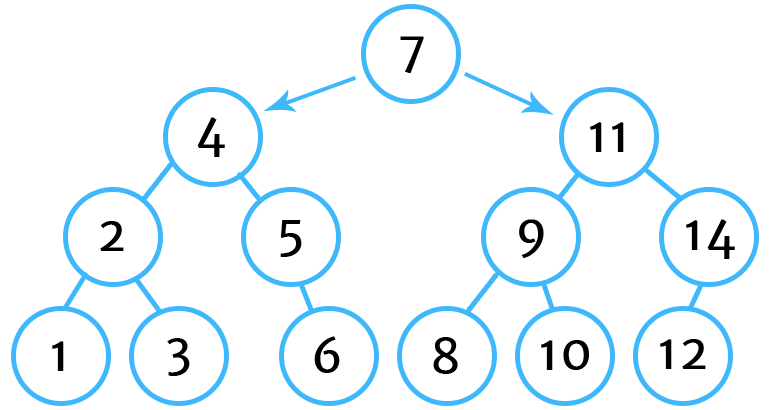
And here is what we will have built by the end of this exercise:
JavaScript
function Node(key) {
this.key = key
this.parent = null
this.height = 1
this.size = 1
this.depth = 0
this.left = null
this.right = null
}Hey, Tyler here. I'm currently working on some great web development and digital marketing products and services over at ZeroToDigital.
If that sounds interesting to you, please check it out!
The first thing that we need to do is set up our Node class that will accept the parameter key and set it's key equal to that parameter. Each node will hold the following information:
JavaScript
function Tree(key) {
var node = new Node(key)
this.root = node
}Next, we'll create our Tree class. Since a tree is just a data structure containing nodes, the only variable we need to keep track of is the tree's root. We'll also accept key as a paramater and use that to create the first node in our tree.
JavaScript
Tree.prototype.find = function(k, R) {
if (R.key == k) { // If equal to root key
return R
} else if (k < R.key) { // If less than root key
if (R.left) { // If left child is not null
return this.find(k, R.left)
}
return R // If no left child, return place
} else if (k > R.key) { // If greater than root key
if (R.right) { // If right child is not null
return this.find(k, R.right)
}
return R // If no right child, return place
}
}Our first function belonging to our tree will be our find function that we'll use to traverse through our tree to find a specific node. This function will accept k - the value of our node (in this tree, the value will always be a node's key), and R -the root of our tree.
If the key is the root's key, then we'll return the root as being found. If the key is less than the root's key and it has a left child, we'll continue our search in the node's left child. If the left child doesn't exist we'll return the current node which we'll use as the placeholder for where our next node should go.
If the key is greater than the root's key and the root has a right child, we'll continue our search in the node's right child. If the right child doesn't exist we'll return the current node as a placeholder.
JavaScript
Tree.prototype.rangeSearch = function(x,y) {
var L = [] // Array to store our results
var N = this.find(x, this.root) // Turn x into node
while (N.key <= y) { // If new node's key is less than or equal to y
if (N.key >= x) { // If new node's key is greater than or equal to x
L.push(N) // Add to array
}
N = this.next(N) // Continue in range
}
return L // Return array of results
}Now we want the ability to find and return a range of nodes. We can do this by creating a functioned called rangeSearch that will accept 2 values, x and y to search between. First, we'll create an empty array of L to hold our array of results. Then, we'll use our find function that we just declared to return the first found node in our range. Then we'll check to see if it's key is less than or equal to y - the top of our range. While it is, if it's greater than or equal to the bottom of our range we'll push it to our results array.
Then we'll return our results array of L.
You'll notice we called a new function inside of rangeSearch. Let's declare that below.
JavaScript
Tree.prototype.next = function(N) {
if (!N.key) {
var N = this.find(N, this.root)
}
if (N.right) {
return this.leftDescendant(N.right) // If right child exists, get descendant
} else {
return this.rightAncestor(N) // Else get ancestor
}
}The next function will be used to find the next node in our tree when given a node - which we'll do by giving the function an initial paramater of N. If N isn't a node already, use the find function to set it as a node.
If the node has a right child, find the left descendant of that child. Else, find the right ancestor of the current node.
We called 2 new functions. Let's break them down.
JavaScript
Tree.prototype.leftDescendant = function(N) {
if (!N.left) { // If no left child, return
return N
} else {
return this.leftDescendant(N.left) // Else find descendant of left child
}
}With our leftDescendant function, we'll see if the node has a left child. If it doesn't we'll just return the current node. If it does, we'll recurse the function on the node's left child.
JavaScript
Tree.prototype.rightAncestor = function(N) {
if (N.parent) { // If parent is not null
if (N.key < N.parent.key) { // If node's key is less than parent's key
return N.parent // Return parent
} else {
return this.rightAncestor(N.parent) // Else find ancestor of parent
}
}
}The rightAncestor function will be used to find the next node based on the current node's parent. If the current node has a parent, we'll check to see if the current node's key is less than its parent's key. If it is, we'll return the parent. If it isn't, we'll recurse the function on the parent node.
JavaScript
Tree.prototype.insert = function(k) {
P = this.find(k,this.root) // Get place to insert node
var node = new Node(k) // Create new node
node.parent = P // Set parent
node.parent.size++ // Increment size of parent
if (P && k > P.key) { // If new value is greater than place
P.right = node // Set parent's right child to new node
} else {
P.left = node // Set parent's left child to new node
}
return node // Return new node
}Now we need to way to inset new nodes into our tree, so we'll create a new insert function. This function will accept a parameter k which will hold the value (key) of our new node. Then, we'll call the find function to locate the place where our new node should be located. Once we've determined that, we'll create the new node based on the value submitted, set the node's parent to P - the place, increase the size of the parent to account for the added node, and then, whether the new node is bigger or less than the value of the parent, we'll add it as a child node of the parent. Finally, we'll return the new node.
This function inserts a new node into our tree, but it doesn't keep the tree balanced when doing so. In fact, if we use this function as-is to insert a bunch of nodes, we could end up with something like this:
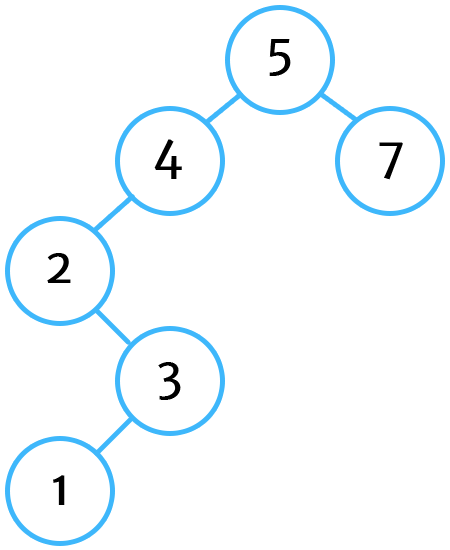
This won't work for our binary tree implementation because, for efficiency purposes, we want the sizes of the root nodes children to be the same (or within 1). So we're going to add a new function upon insertion that will keep our tree balanced.
JavaScript
Tree.prototype.avlInsert = function(k) {
var N = this.insert(k, this.root) // Set N equal to insertion of new node
this.adjustDepth(N) // Adjust depth of the new node
this.rebalance(N) // Rebalance tree based on node size
}Our new avlInsert function will insert new nodes via the previous insert function we just created, but afterward it will do 2 things - adjust the depth of the new node and then rebalance it.
JavaScript
Tree.prototype.rebalance = function(N) {
if (N.parent) { // If node has parent, set equal to P
var P = N.parent
}
if (N.left && N.right) { // If node has both a left and right
if (N.left.size > N.right.size + 1) { // If left size is greater than right size plus 1
this.rebalanceRight(N) // Rebalance on the right side
}
if (N.right.size > N.left.size + 1) { // If right size is greater than left size plus 1
this.rebalanceLeft(N) // Rebalance on the left side
}
} else if (N.left && N.left.size > 1) { // If no right child but left size is greater than 1
this.rebalanceRight(N) // Rebalance on the right side
} else if (N.right && N.right.size > 1) { // If no left child but right size is greater than 1
this.rebalanceLeft(N) // Rebalance on the left side
}
this.adjustHeight(N) // Update heights
this.adjustDepth(N) // Update depths
if (P) { // If node had parent, recurse rebalance function with parent
this.rebalance(P)
}
}The main purpose of our rebalance function is to determine where the tree is unbalanced by looking at node sizes and then calling a few new functions to rebalance the tree post the addition of the new node.
If the node's left child's size is greater than it's right child's size plus 1 then it's unbalanced, and we need to call the rebalanceRight function. If the node doesn't have a right child and the size of it's left child is greater than 1, then we'll call the same function.
If the opposites are true, then we'll call the rebalanceLeft function.
After we balance the children, we'll readjust the height and depth of the node to account for the changes, then recurse up to check the balance of the node's parent.
JavaScript
Tree.prototype.rebalanceRight = function(N) {
var M = N.left // Set M equal to node's left child
if (M.right && M.left && M.right.size > M.left.size) { // If M has both right and left children and M's right size is greater than it's left size
this.rotateLeft(M) // Rotate left on M
} else if (M.right && M.right.size > 1) { // If M has a right child and it's size is more than 1
this.rotateLeft(M) // Rotate left on M
}
this.rotateRight(N) // Rotate right on N
}
Tree.prototype.rebalanceLeft = function(N) {
var M = N.right // Set M equal to node's right child
if (M.right && M.left && M.left.size > M.right.size) { // If M has both right and left children and M's left size is greater than M's right size
this.rotateRight(M) // Rotate right on M
} else if (M.left && M.left.size > 1) { // If M has a left child and it's size is more than 1
this.rotateRight(M) // Rotate right on M
}
this.rotateLeft(N) // Rotate left on N
}We'll call the rebalanceRight and rebalanceLeft functions together since they're mirror-images of eachother, and we'll walk through the first one.
In the rebalanceRight function, we'll set the variable M equal to the node's left child. Then we'll check to see if M has a right and left child and if the right child's size is bigger than the left child's. If so, or if M doesn't have a left child and the size of it's right child is bigger than 1, we'll rotate the node to the left. Then, we'll rotate the original node -N - to the right.
JavaScript
Tree.prototype.rotateRight = function(X) {
var P = X.parent // P is parent of current node
var Y = X.left // Y is current node's left child
var B = Y.right // B is Y's right child
Y.parent = P // Set Y's parent equal to X's parent
if (Y && P) { // If Y and P not null
if(Y.key > P.key) { // If Y bigger than P - X's parent
P.right = Y // X's parent's right child equal to Y
} else {
P.left = Y // X's parent's left child equal to Y
}
}
if (X.parent == null) { // If X is current root node
this.root = Y // Set Y as the tree's new root
}
X.parent = Y // Set X's new parent to Y
X.left = B // Set's X's left child to B
Y.right = X // Set Y's right child to X
if (B) { // If Y has a right child
B.parent = X // Set it's parent to X
}
this.recomputeSize(X) // Recompute size of X
this.recomputeSize(Y) // Recompute size of Y
if (P) { // If P or X's parent is not null
this.recomputeSize(P) // Recompute size of P
}
}
Tree.prototype.rotateLeft = function(X) {
var P = X.parent // P is parent of current node
var Y = X.right // Y is current node's right child
var B = Y.left // 8 is Y's left child
Y.parent = P // Set Y's parent equal to P - X's parent
if (Y && P) { // If Y and P not null
if (Y.key > P.key) { // If Y greater than P
P.right = Y // Set X's parent's right child equal to Y
} else {
P.left = Y // Set X's parent's left child equal to Y
}
}
if (X.parent == null) { // If X is current root node
this.root = Y // Set Y as the tree's new root
}
X.parent = Y // Set X's new parent as Y
Y.left = X // Set Y's left child as X
if (B) { // If Y has a left child
B.parent = X // Set Y's left child equal to X
}
X.right = B // Set X's right child equal to B - Y's former left child
this.recomputeSize(X) // Recompute size of X
this.recomputeSize(Y) // Recompute size of Y
if (P) { // If P or X's parent is not null
this.recomputeSize(P) // Recompute size of P
}
}We'll also call the rotateRight and rotateLeft functions together since they are mirror-images of each other. Let's go through the rotateRight function together.
It looks like a lot here, but really we're just reassigning parent and child nodes. We're going to set P equal to the parent of X , Y equal to X's left child, and B equal to Y's right child. Then Y's parent is now going to be P and if Y is bigger than P it'll be it's right child - otherwise, it's left child.
If X's parent is null then that means it's currently the tree's root node. We're going to change that and set the root of the tree equal to Y. X's new parent is now Y and it's left child has been changed from Y to B. Meanwhile, Y's right child has been changed to X. If B is not null, then it's parent is set to X.
Now that we've reassigned the nodes, we need to call the recomputeSize function on the affected nodes - X, Y and, if it exists, P.
The rotateLeft function is the same but opposite - refer to the many comments added in the code for help and organization purposes!
JavaScript
Tree.prototype.recomputeSize = function(N) {
var size = 1 // Start with size of 1
if (N.left) { // If node has left child
size += N.left.size // Add size of left child
}
if (N.right) { // If node has right child
size += N.right.size // Add size of right child
}
N.size = size // Set node's size equal to size variable
}As called in the rotate functions, recomputeSize takes a node and recomputes its size based on its children nodes plus 1 (to include itself).
JavaScript
Tree.prototype.adjustHeight = function(N) {
if (N.left && N.right) { // If both left and right children
N.height = 1 + Math.max(N.left.height, N.right.height) // New height is 1 plus the max between the left and right heights
} else if (N.left) { // If not both, but left child exists
N.height = 1 + N.left.height // New height is 1 plus height of left child
} else if (N.right) { // If not both but right child exists
N.height = 1 + N.right.height // New height is 1 plus height of right child
} else {
N.height = 1 // If no children, new height is 1
}
if (N.parent) { // Recurse adjustHeight on parent till root node
this.adjustHeight(N.parent)
}
}In addition to the previous function that recomputes the size of the node, we also need to cover the adjustHeight and adjustDepth functions that were first called in the rebalance function.
This function updates the height of the node based on the heights of its children. A node's height is the height of its tallest child plus 1 (to include itself). We'll just JavaScript's native Math.max function to determine which child is taller if they both exist.
JavaScript
Tree.prototype.adjustDepth = function(N) {
if (N.key < this.root.key) { // If this node is on the left side of the tree
N.depth = this.root.left.height - N.height + 1 // New depth is height of root's left child - height of current node plus 1
} else if (N.key > this.root.key) { // If this node is on right side of tree
N.depth = this.root.right.height - N.height + 1 // New depth is height of root's right child - height of current node plus 1
} else if (N.key == this.root.key) { // If node is root
N.depth = 0 // New depth is 0
}
if (N.right) { // If node has right child, recurse adjustDepth function
this.adjustDepth(N.right)
}
if (N.left) { // If node has left child, recurse adjustDepth function
this.adjustDepth(N.left)
}
}Our adjustDepth function will calculate the depth of the given node. The depth is the node's distance away from the root of the tree. So, to calculate this, we'll use the height of the root node's left or right child (depending on what side of the tree the current node exists on) and subtract the current node's height from it and add 1 to get our depth. Then we'll recurse to the node's children to update them as well.
JavaScript
Tree.prototype.delete = function(N) {
if (!N.key) {
var N = this.find(N, this.root) // Set N equal to node of key N
}
if (N.right) { // If node has a right child
if (N.right.key > N.parent.key) { // If node's right key is greater than node's parent key
N.parent.right = N.right // Set parent's right equal to replacing node
} else {
N.parent.left = N.right // Else set parent's left equal to replacing node
}
N.right.parent = N.parent // Set the parent of the replacing node
N.right.depth-- // Reduce it's depth by 1
} else if (N.left) { // Else if node has left child
if (N.left.key > N.parent.key) { // If node's left key is greater than node's parent key
N.parent.right = N.left // Set parent's right equal to replacing node
} else {
N.parent.left = N.left // Else set parent's left equal to replacing node
}
N.left.parent = N.parent // Set the parent of the replacing node
N.left.depth-- // Reduce it's depth by 1
}
var temp = N // Set temp equal to node to be deleted
delete N // Delete node
return temp // Return deleted node
}We may also need to delete a node at times so let's add a function to do that.
The delete function isn't as simple as just removing a node because it could potentially break our tree if the node has child nodes. So we need to delete the node and declare a node to take it's place. If the node has a right child, we'll start there and compare it to the original node's parent. If not, we'll try the left node. Then we'll set the original node equal to the temp variable before deleting so that we can return the deleted node.
But this could still potentially mess up our tree - or at least the balance of it. So we need to add a way for nodes to be deleted while maintaining balance.
JavaScript
Tree.prototype.avlDelete = function(N) {
var N = this.find(N, this.root) // Create node from inserted value
var M = N.parent // Set M equal to node's parent
this.delete(N) // Delete node using delete function
this.rebalance(M) // Rebalance tree with M
}In our avlDelete function, we'll find the node containing the submitted key, and then we'll find it's parent. Then we'll call the delete function on the node and the rebalance function on it's parent - M.
JavaScript
Tree.prototype.orderStatistic = function(R, k) { in the tree
if (R.left) { // If root node has left child
var s = R.left.size // Set s equal to size of left child
} else {
var s = 0 // Set s equal to 0
}
if (!k.key) { // If not node, set k equal to its node
var k = this.find(k, R)
}
if (k.size == s + 1) { // If k's size is equal to s + 1
return R // Return the root node
} else if (k.size < s + 1) { // If k is less, recurse the function with the root's left size
return this.orderStatistic(R.left, k)
} else if (k.size > s + 1) { // If k is greater, recurse the function with the root's right side
return this.orderStatistic(R.right, k.size - s - 1)
}
}With our orderStatistic function we can return the kth smallest element (and determine the rank of a node) in our tree (kth referring to the value for k that we're submitting). This allows us to emulate the functionality of an Order Statistic Tree in our binary tree in O(log n) time.
Here, we'll recurse the function looking for the node with the matching size of k starting with the tree's root.
JavaScript
Tree.prototype.rangeSum = function(x,y) {
var range = this.rangeSearch(x,y) // Get array of nodes in range
var sum = 0 // Set sum equal to 0
for (i = 0; i < range.length; i++) { // Loop through nodes in range
sum += range[i].key // Increase sum per keys
}
return sum // Return result
}Finally, we'll call a simple rangeSum function to, in this scenario, leverage the previously declared rangeSearch function to return an array of nodes that fall within the given range, and then iterate through the results and sum up the key values.
This would be a simple way to sum or concatenate values in a range regardless of data type - integer, string, or other.
JavaScript
var tree = new Tree(5)
tree.avlInsert(4)
tree.avlInsert(2)
tree.avlInsert(3)
tree.avlInsert(7)
tree.avlInsert(1)
tree.avlInsert(6)
tree.avlInsert(9)
tree.avlInsert(8)
tree.avlInsert(10)
tree.avlInsert(11)
tree.avlInsert(14)
tree.avlInsert(12)Finally, we can create our tree, insert into it, delete from it, find nodes in it, and many of the other functions we mentioned above. After inserting the above nodes, our tree should be organized like how it is in the picture at the beginning of our post.