A hash table, by definition, is an unordered collection of key-value pairs where each key is unique. In a previous post, I showed how you could implement direct address hashing to look up values by using a key. The reason why you'd want to do this is so that you could search for a value in constant time - O(1) - just like you can with an array, and do so by using a meaningful key value, regardless of size.
In this implementation, we're going to take that example a step further and leverage probingto help us in instances of collision and to help us to increase and decrease the size of our hash table for efficiency and memory purposes.
Hey, Tyler here. I’m building Formyra, an AI-powered smart forms platform that helps businesses automate workflows, cut busywork, and turn form submissions into real growth.
If that sounds interesting, I’d love for you to check it out!
JavaScript
function phoneBook(size) {
this.count = 0 // to keep track of the actual item count in our table
this.size = size // the current storage size of our table
this.maxLoadFactor = 0.667 // when our table crosses the 2/3rds capacity, the size will either need to be increased or decreased
this.increaseBy = 1.5 // when our table size is changed, this factor determines how large the charge will be
this.table = new Array(size) // the table that will hold our keys and values
}Again, we'll be building off of our phone book direct address hashing implementation that we built previously, but you don't need to have read that post as I'll walk through this entire implementation step by step.
We'll need to create a phone book class that will accept a parameter of size. This will allow a user to implement a size of their choice when using this class. As opposed to our previous example, we don't need to set a gigantic size up front because we're going to cover how to increase the size of our hash table as we go along and that's where the maxLoadFactor and increaseBy variables come in to play. The maxLoadFactor (which we've preset at 0.667) will be the threshold that we'll use for when resizing our table will be necessary. When our table is more than 2/3rds full, we'll need to increase the size. When we remove items and the table is less than 2/3rds full, we'll decrease the size.
The maxLoadFactor variable determines by how much we'll increase or decrease the size of our table. You could designate a number larger or smaller than this, but we don't want to make our table too big because then it could be taking up a large amount of unused memory. On the contrary, if we increase the size of our table by too little then we'll have to run our resizing functions more frequently which we'd have to account for in efficiency.
Finally, our table variable will be an array of the size we declared to hold our key-value pairs.
JavaScript
phoneBook.prototype.hash = function(x) {
var a = 113 // random number between 1 and p - 1
var b = 87 // random number between 1 and p - 1
var p = 10000019 // prime number - the higher the more unique
var m = this.size // hash table rows
return ((a * x + b) % p) % m // return result of hash formula
}We'll create a hash function to take keys as parameters and return a hashed value. This is a JavaScript implementation of the universal hash function whose formula depends on 5 values:
We'll take these values, run them through the formula, and return the hashed result.
JavaScript
phoneBook.prototype.add = function(key, value) { // Constant Time
var key = key.replace(/-/g, '') // replace hyphens from key input
var hash = this.hash(key) // create hash value out of key
if (this.table[hash]) { // if position is already filled
if (this.table[hash].key == key) { // if table position's key matches
this.table[hash].value = value // update value
} else {
var val = this.probe(hash)
this.table[val] = {key, value} // then place key and value in found empty position
this.count++ // increment count of phone book after adding value
}
} else { // ff position empty
this.table[hash] = {key, value} // place key and value in found empty position
this.count++ // increment count of phone book after adding value
}
if (this.count >= (this.size * this.maxLoadFactor)) { // if phone book is full
this.increaseSize() // call function to increase size of table
}
}The add function will allow us to input new key-value pairs in our table. It accepts a key and value as parameters then cleans the key value (since we're dealing with phone numbers, we'll remove any hyphens inputted by the user) and calls the hash function to create a hashed key value (you'll see this pattern repeated in a few other functions to follow).
Then we'll need to add our new key and value to the hash table. We'll first check if anything exists at the index value of our hash. If not, then we can add our new key-value pair at that location and increase the count of our hash table. However, if something is already taking up that position in our table, we'll then check if it has the same exact key. If it does, then we'll just update the value with our new value. If the keys don't match, then we'll have to probe until we can find an empty table position for our new value.
We'll walk through our probing function next, but basically, we're adding a formula to our hashed value which will walk us through our array until we find an empty location.
When we've located an empty position, we'll add our key-value pair to that position. After doing that, we need to check to see if by adding our new value we've crossed our max capacity, or maxLoadFactor of 0.667. If yes, we'll need to run a function to increase the size of our table. More to come.
JavaScript
phoneBook.prototype.probe = function(hash) {
var a = 1; // 1 or where GCD of size and a is 1
var i = 0 // counter to use for incrementing
var val = (hash + (a * i)) % this.size // get value with probe of 0
while (this.table[val]) { // while table's position is filled
i++ // increment i
val = (hash + (a * i)) % this.size // probe next position
}
return val // return the result of the hash and probe function that results in an empty table position
}Our probe function will walk us through our table until we've found an empty position that can accept a new value. It will accept a parameter of hash (a hashed key value), and will declare a value for a which can be 1 or any value where the greatest common denominator between itself and the size of the hash table is 1. If the greatest common denominator of the 2 numbers is more than 1 than the loop inside of the probe function could be infinite.
We'll also create a variable i that we'll use as an incrementing counter inside our while loop and create/set a value for val that will be updated as long as the table's position is filled when using val as an index.
Once our loop has ended and we've determined an open position, we'll return that position's index of val.
JavaScript
phoneBook.prototype.increaseSize = function() {
var temp = this.table // set current table equal to temp variable
this.size = this.size * this.increaseBy // increase size of phone book
this.table = new Array(this.size) // create new table with updated size
for (i = 0; i < temp.length; i++) { // loop through current table
if (temp[i]) { // if value in current table at position
var key = temp[i].key // get key at position
var value = temp[i].value // get value at position
var hash = this.hash(key) // hash key value
if (this.table[hash]) { // if position is already filled
var val = this.probe(hash) // get new hash value returned from probe function
this.table[val] = {key, value} // then place key and value in found empty position
} else { // if position empty
this.table[hash] = {key, value} // place key and value in found empty position
}
}
}
}If we exceed the preset maxLoadFactor of our table, then we'll need to increase its size. To do that, we'll create a function called increaseSize that won't take any arguments, but will set the variable temp equal to the existing table, increase the table's size variable by multiplying it by the table'sincreaseBy variable, and then set the table variable equal to a new array of the updated size. We'll then create a simple for loop to loop through all of the values now in our temp array (omitting the empty array items). We'll capture the key and value from the array position and then hash our key.
With our hashed key value, we'll check to see if the position is already occupied in our newly-created table. If it is, we'll need to call our probe function to search our table for an empty position. Once that has been found, we'll place our key-value pair there.
While many operations in a hash table are constant, increasing and decreasing size are not. Since we need to rehash and relocate every existing value in our table, we'll need linear time - O(n) - to complete the operation. We also can't ignore the fact that rehashing each key value will take a toll as well. So we can more accurately describe our increaseSize function as having Θ(nH) time - or big-theta of n multiplied by the time it will take to run our hash function. This isn't very efficient and, if efficiency is something that you value over memory, then this would be a good reason to increase the increaseBy value to perhaps double the size of the table each time the maxLoadFactor capacity is crossed.
JavaScript
phoneBook.prototype.get = function(key) {
var key = key.replace(/-| /g, '') // replace hyphens from key input
var hash = this.hash(key) // create hash value out of key
var a = 1; // probe a - 1 or where GCD of size and a is 1
var i = 0 // counter for probe
var val = (hash + (a * i)) % this.size // initial probe value with probe of 0
if (this.table[hash]) { // if table position is already filled
if (this.table[hash].key == key) { // if position's key matches
return this.table[hash].value // return value
} else {
while (this.table[val]) { // while table position contains value
if (this.table[val].key == key) { // if key matches
return this.table[val].value // return value
}
i++ // Increment i
val = (hash + (a * i)) % this.size // Probe next position
}
console.log('Number Not Found')
}
}
}To return a value from our hash table, we'll create the get function that will accept an argument of key. We'll hash the key and then copy some of the code from our probe function to search through our table until the hashed key value is discovered. The reason why we can't just use the actual probe function here is because we're probing for a specific key, not for an empty table position. Once we've found the key, we'll return the value.
This operation can be done in near constant time. Frequently, it will be constant time. However, it won't be when we have to probe through the table when the original hashed value's key doesn't match.
JavaScript
phoneBook.prototype.remove = function(key) { // Constant Time
var key = key.replace(/-| /g, '') // remove hyphens from key input
var hash = this.hash(key) // create hash value of key
var a = 1; // probe a - 1 or where GCD of size and a is 1
var i = 0 // counter for probe
var val = (hash + (a * i)) % this.size // probe value with probe of 0
if (this.table[hash]) { // if table position has value
if (this.table[hash].key == key) { // if key matches
delete this.table[hash] // delete value at position
this.count-- // decrement count
} else {
while (this.table[val]) { // while position has value
if (this.table[val].key == key) { // if key matches
delete this.table[val] // delete value at position
this.count-- // decrement count
break // break out of loop
}
i++ // increment i for probe
val = (hash + (a * i)) % this.size // probe next position
}
console.log('Number Not Found') // log message
}
} else {
console.log('Number Not Found') // log message
}
if (this.count < (this.size * this.maxLoadFactor)) { // if count decreased below load factor
this.decreaseSize() // call function to decrease size of table
}
}What if we need to remove values from our hash table? We can do that with our remove function. This function is very similar to our previous get function. In fact, the only difference is that when we find the key we're looking for we delete the data from the table and decrement the count of our table by 1. Then, just like the add function, we check if the count of the table has crossed the maxLoadFactor line. This time, if it has we'll call our decreaseSize function to reduce the size of the table.
JavaScript
phoneBook.prototype.decreaseSize = function() {
var temp = this.table // set current table equal to temp variable
this.size = this.size / this.increaseBy // decrease size of phone book
this.table = new Array(this.size) // create new table with updated size
for (i = 0; i < temp.length; i++) { // loop through current table
if (temp[i]) { // ff value in current table at position
var key = temp[i].key // get key at position
var value = temp[i].value // get value at position
var hash = this.hash(key) // hash key value
if (this.table[hash]) { // ff position is already filled
var val = this.probe(hash) // get new hash value returned from probe function
this.table[val] = {key, value} // then place key and value in found empty position
} else { // if position empty
this.table[hash] = {key, value} // place key and value in found empty position
}
}
}
}And our decreaseSize function is a mirror-image of our increaseSize function except that we're dividing the current size by the increaseBy variable. Once we do that, we'll follow the same operations to put the temp variables values into the new array.
JavaScript
var phoneBook = new phoneBook(4)
phoneBook.add('911', 'Police')
phoneBook.add('012-345-6789', 'Mom')
phoneBook.add('987-654-3210', 'Dad')
phoneBook.add('555-555-5555', 'Sam')
phoneBook.add('999-999-9999', 'Tommy')
phoneBook.add('123-123-1234', 'Sandra')
phoneBook.add('123-123-1234', 'Sandy') // updates value
phoneBook.remove('9999999999') // removes Tommy
phoneBook.add('456-456-4567', 'Phillip')
console.log(phoneBook.get('911')) // Police
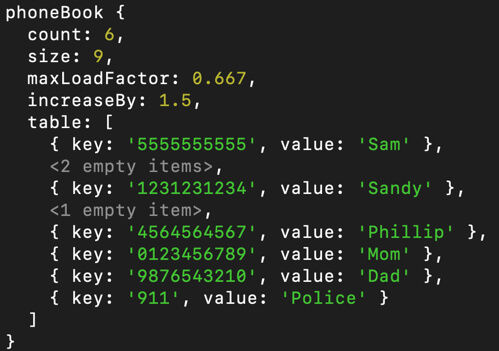
console.log(phoneBook) // logs image belowNow we can implement our new phoneBook class. We'll create a new phone book of size 4, and then add a few phone numbers and names into our table. Then we'll remove a value and get another. Below is how this phone book now looks in the console:
Tweet me @tylerewillis