Find Inorder Successor in Binary Search Tree

Use Case:

When we've implemented a binary search tree, there could be situations when, given a node or a value, we need to locate and return the value of the next node or value in a given set of data. Maybe we've built a program that returns data in order to a user and they need the next piece of data, we need a way for them to be able to do that.

Even though trees aren't linear data structures like arrays and linked lists, we can still create ways to return the values sequentially - and faster than linear data structures in logarithmic - O(log n) - time.

In this post, we're going to create 4 functions - 3 of which are recursive - that will allow us to do this, regardless of the value. One thing to note, however, is that if the value submitted is already the greatest value in our tree data structure, then our algorithm below will return null.

Also, we're going to be using a class calledTree that we created in a previous post outlining a complete implementation of a binary search tree. Please read up on that post if the below is confusing or difficult to grasp.

getSuccessor Function

Our first function will be used to manage the overall algorithm of finding the successor of a value.

Tree.prototype.getSuccessor = function(N) {
	if (!N.key) var N = this.find(N, this.root)
	if (N.right) return this.leftDescendant(N.right)
return this.rightAncestor(N)
}

The getSuccessor function will accept a node and first check if the node is a valid node with a key. If it's not, then we'll find the node that equals our value by calling the find function. The reason for this first line is so that when you call this function later, it'll be easier for you to just submit a value instead of needing to submit an actual node. Way easier!

After setting our value of N, we'll check if the node has a right child. If it does, we'll return the value of that child's left descendant (since, in a true binary search tree, every node to the right should be greater than the current node). If not, we'll return a right ancestor of the existing node. I know, I'm speaking in tongues. Keep going ...

find Function

Tree.prototype.find = function(k, R) {
	if (R.key == k) {
		return R
	} else if (k < R.key) {
		if (R.left) return this.find(k, R.left)
		return R
	} else if (k > R.key) {
		if (R.right) return this.find(k, R.right)
		return R
	}
}

Our find function (called in our previous function) is a recursive function that will recurse until it's located a node whose key matches the value we're looking for. First, it'll check if the current node matches (R, which is the root of the tree). If it does, it'll return that node. If not, since our data structure is a binary search tree, it'll cut the data set in half by determining if the value we're searching for is less than or greater than our tree's root. Then it'll recurse on the root's left or right child.

Eventually, after our data set will be halfed and then halfed again, we'll get a node for our submitted value in our getSuccessor function.

leftDescendant Function

Tree.prototype.leftDescendant = function(N) {
	if (!N.left) return N
	return this.leftDescendant(N.left)
}

Our leftDescendant function will accept a node and check to see whether that node has a valid left child. If it doesn't, it'll return the current node. If it does, it'll recurse on the node's left child.

If you recall back to our getSuccessor function, we've determined that the original node had a right child. So we're trying to find the lowest, left-most leaf belonging to the right child as that would be the next greatest value to our original value.

rightAncestor Function

Tree.prototype.rightAncestor = function(N) {
	if (N.parent) {
		if (N.key < N.parent.key) return N.parent
		return this.rightAncestor(N.parent)
	}
	return null
}

Our rightAncestor function is only called if the original node doesn't have a valid right child. In that case, we have to go up in our tree closer to the root to find our next greatest value.

This function checks if the current node has a parent (it only wouldn't if it was the tree's root). If it does have a parent, then we'll check if the node's key is less than the parent's key and then return the parent. If the node's key is actually greater than the parent's key, then we'll need to look further up to the grandparent and so on and we can do this by recursing the function on the parent node.

Results

Using our previously created tree data structure :

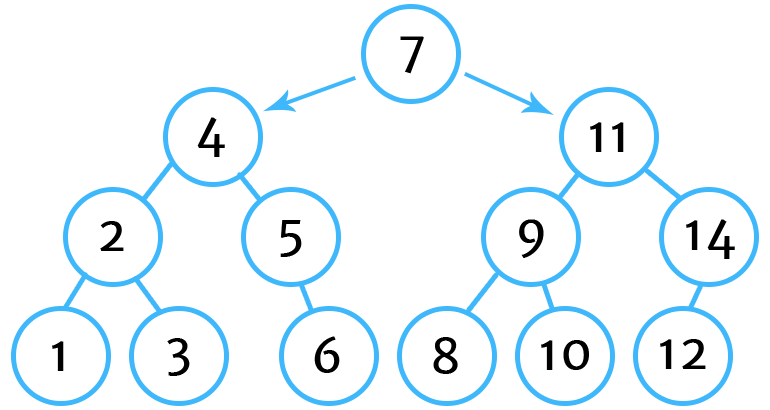
We would get the following results when using this algorithm:

tree.getSuccessor(12) // 14
tree.getSuccessor(1) // 2
tree.getSuccessor(7) // 8
tree.getSuccessor(6) // 7