Check if Binary Search Tree Structure is Valid

Use Case:

In computer science, binary search trees are very useful data structures because they allow for many common functions such as insertion, deletion and searching to be performed in logarithmic time - O(log n). Binary search trees differ from trees who allow parents to have more than 2 children and from regular binary trees that allow parents to only have 2 children but those children aren't necessary in any sort of order.

In order to be able to fully leverage functions in logarithmic time, we need to be sure that each of our tree nodes are greater than the child to their left and less than the child to their right - and so on down their branches. We're going to cover how to verify the validity of a binary search tree with 1 main and 2 supporting functions in JavaScript. Then, at the end, you'll see an animation of how our algorithm works.

isBinaryTree Function

So we need to create a function to compare values and return true or false - depending on if our tree correctly follows the rules of a binary search tree.

Tree.prototype.isBinaryTree = function(node) {
	if (typeof node == 'undefined') var node = this.root
	if (!node) return true
	if (this.isSubtreeLesser(node.left, node.key)
		&& this.isSubtreeGreater(node.right, node.key)
		&& this.isBinaryTree(node.left)
		&& this.isBinaryTree(node.right)) {
		return true
	}
	return false
}

Our isBinaryTree function accepts the value of a node and is being called on the Tree class that we created previously in our post on implementing a complete binary search tree. I like to make things easy for myself down the road, so I would like to call this function without submitting a node the first time around. So our first line will set the value of node if it is not called, or undefined. Then, since this function is recursive, if there is ever a node submitted that is null (if/when a node doesn't have a left or right child) then we'll just go ahead and return true because that isn't a condition that would make our binary search tree invalid.

Then we'll perform a conditional statement that will return true if 4 functions (3 separate functions) all return true. isBinaryTree is recursed twice, both times on the children of the current node. Then we call 2 new functions - isSubtreeLesser on the node's left child and isSubtreeGreater on the node's right child. In both of these function calls we're also sending in the key (in this case, the key represents our node's value) to the function to use for comparison with the children's keys.

If everything returns true, then we'll return true from our function stating that the tree is in fact a valid binary search tree.

Now let's take a look at the 2 new functions we just called.

isSubtreeLesser Function

Tree.prototype.isSubtreeLesser = function(node, value) {
	if (!node) return true
	if (node.key < value
		&& this.isSubtreeLesser(node.left, value)
		&& this.isSubtreeLesser(node.right, value)) {
		return true
	}
	return false
}

The isSubtreeLesser function takes a node and a value and first checks to see whether the node is null. If it is, the function will just return true since the rules of the search tree would still be consistent. Then, the function will check in a conditional statement if the current node's key (the node's value) is less than the submitted value (which belongs to the key of the parent or ancestor). Then we need to recurse the function on the 2 children of the current node.

If everything returns true, then, in fact, our subtree is lesser than the value of the original node so we'll return true. If not, we'll return false.

isSubtreeGreater Function

Tree.prototype.isSubtreeGreater = function(node, value) {
	if (!node) return true
	if (node.key > value
		&& this.isSubtreeGreater(node.left, value)
		&& this.isSubtreeGreater(node.right, value)) {
		return true
	}
	return false
}

Our 3rd and final function we'll need to verify that our tree data structure is in fact a valid binary search tree is our isSubtreeGreater function. This function is just like our previous function but opposite. Here we'll checking if the current node's key is greater than the submitted value and then recursing the function on the node's children. If everything returns true, we return true from our function.

Results

Here is the order for how our algorithm will traverse and compare values in our tree:

• 1 < 7, 3 < 7, 2 < 7, 6 < 7, 5 < 7, 4 < 7
• 8 > 7, 10 > 7, 9 > 7, 12 > 7, 14 > 7, 11 > 7
• 1 < 4, 3 < 4, 2 < 4
• 6 > 4, 5 > 4
• 1 < 2
• 3 > 2
• 6 > 5
• 8 < 11, 10 < 11, 9 < 11
• 12 > 11, 14 > 11
• 8 < 9
• 10 > 9
• 12 < 14

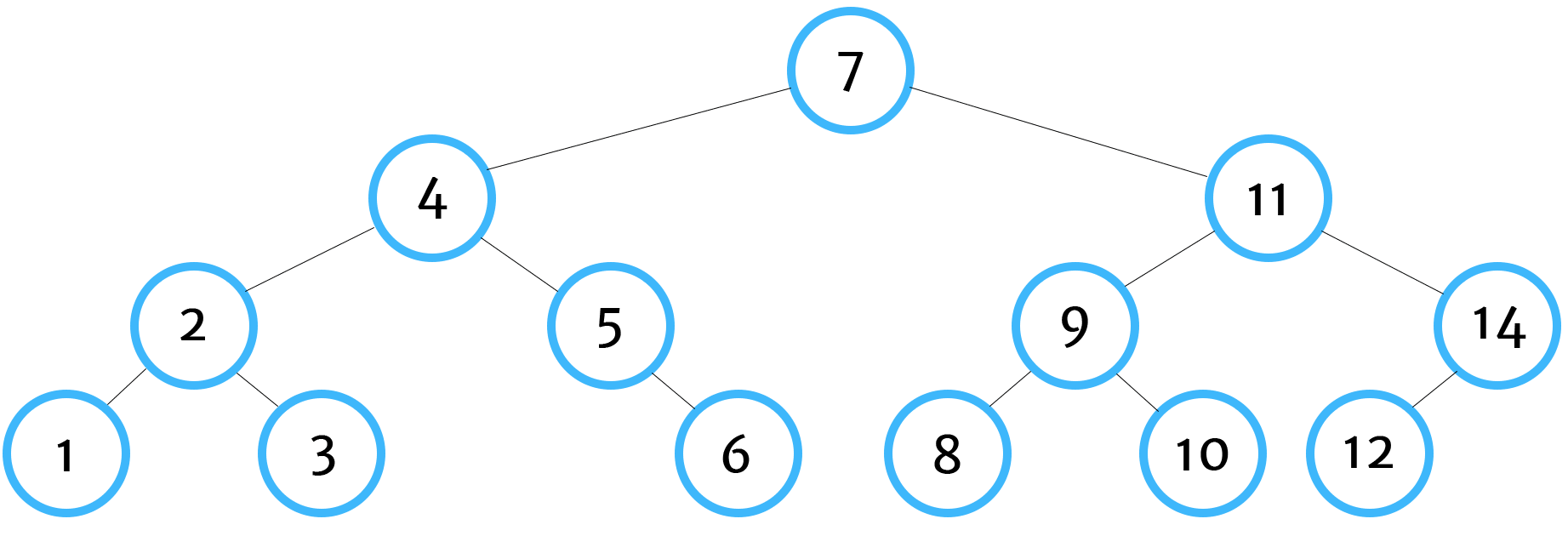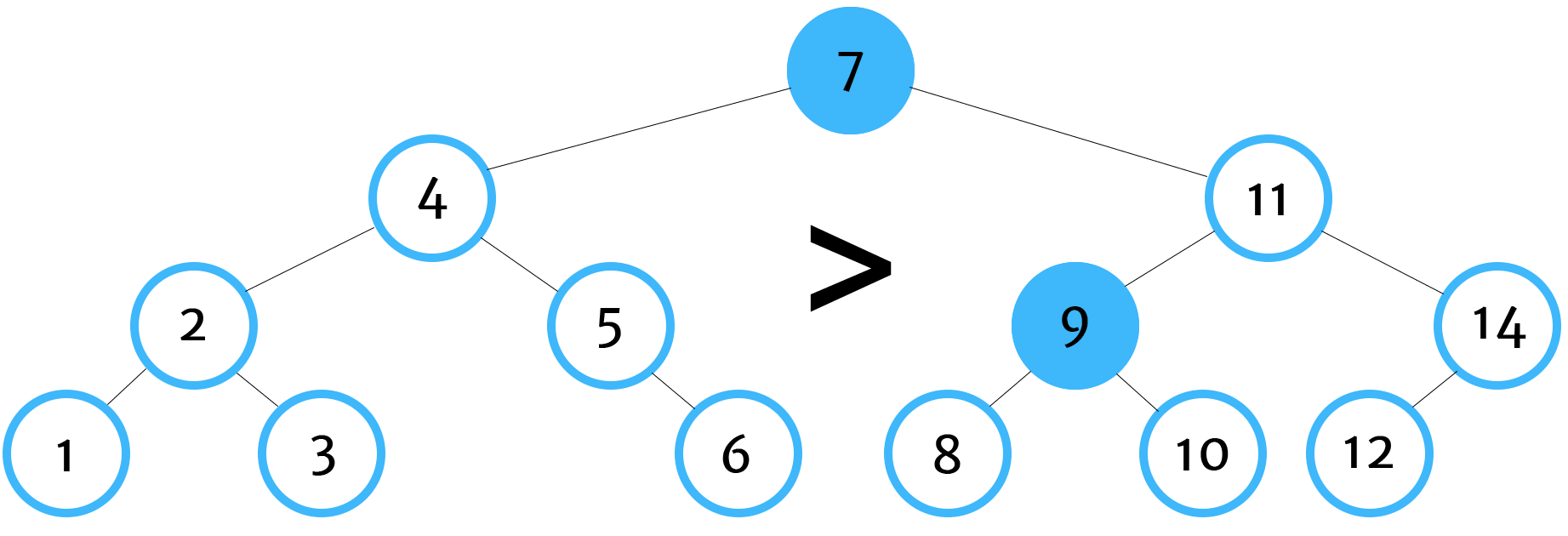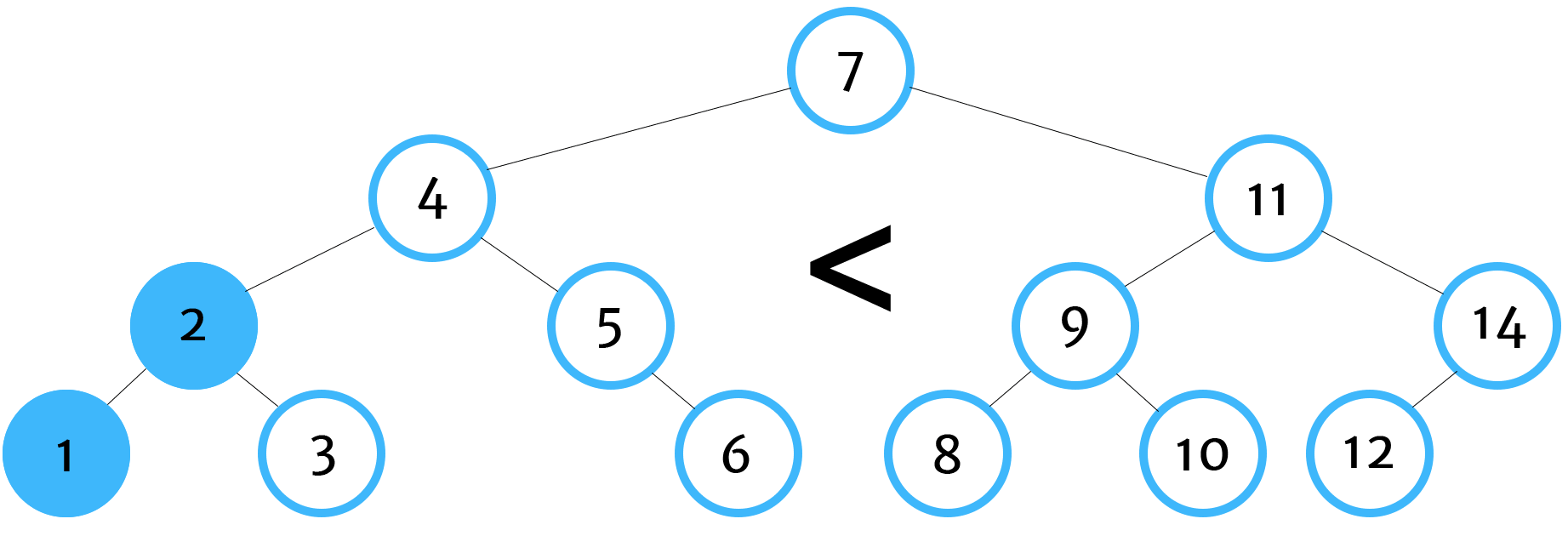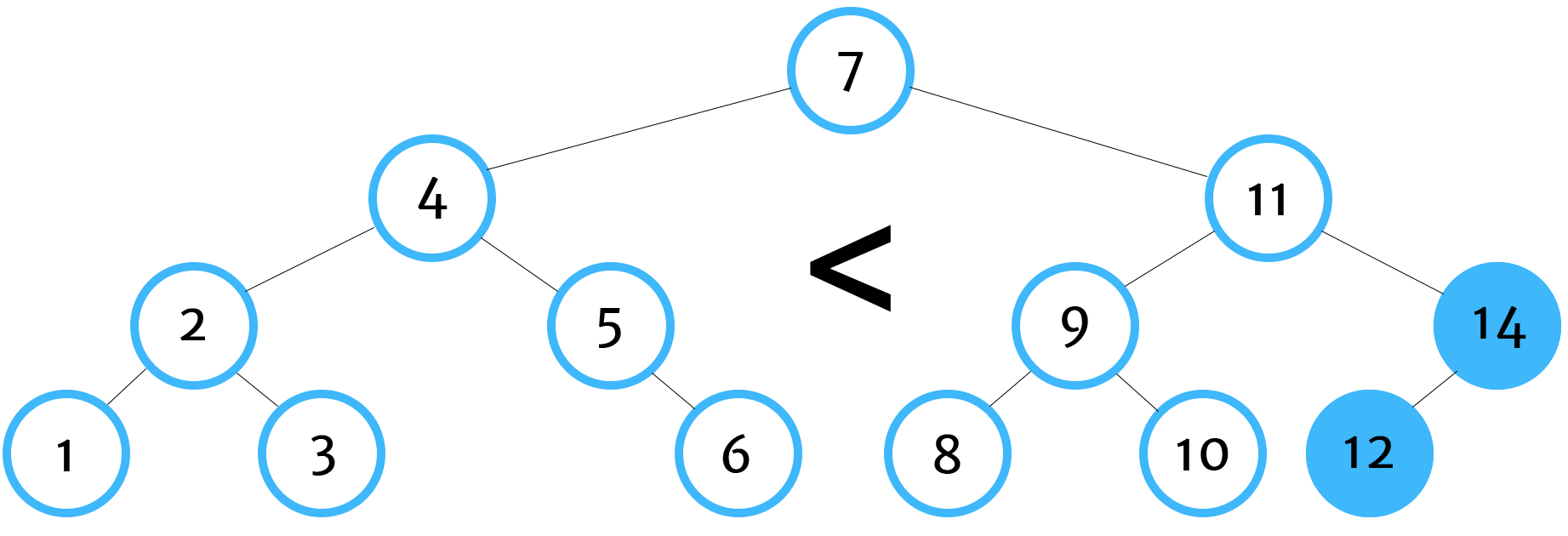
And our algorithm returns true. Again, if you'd like to see how we constructed this binary search tree in JavaScript, take a look at the previous post.